Aumentar a espessura do isolamento aumenta a taxa de transferência de calor? O Raio Crítico Explicado

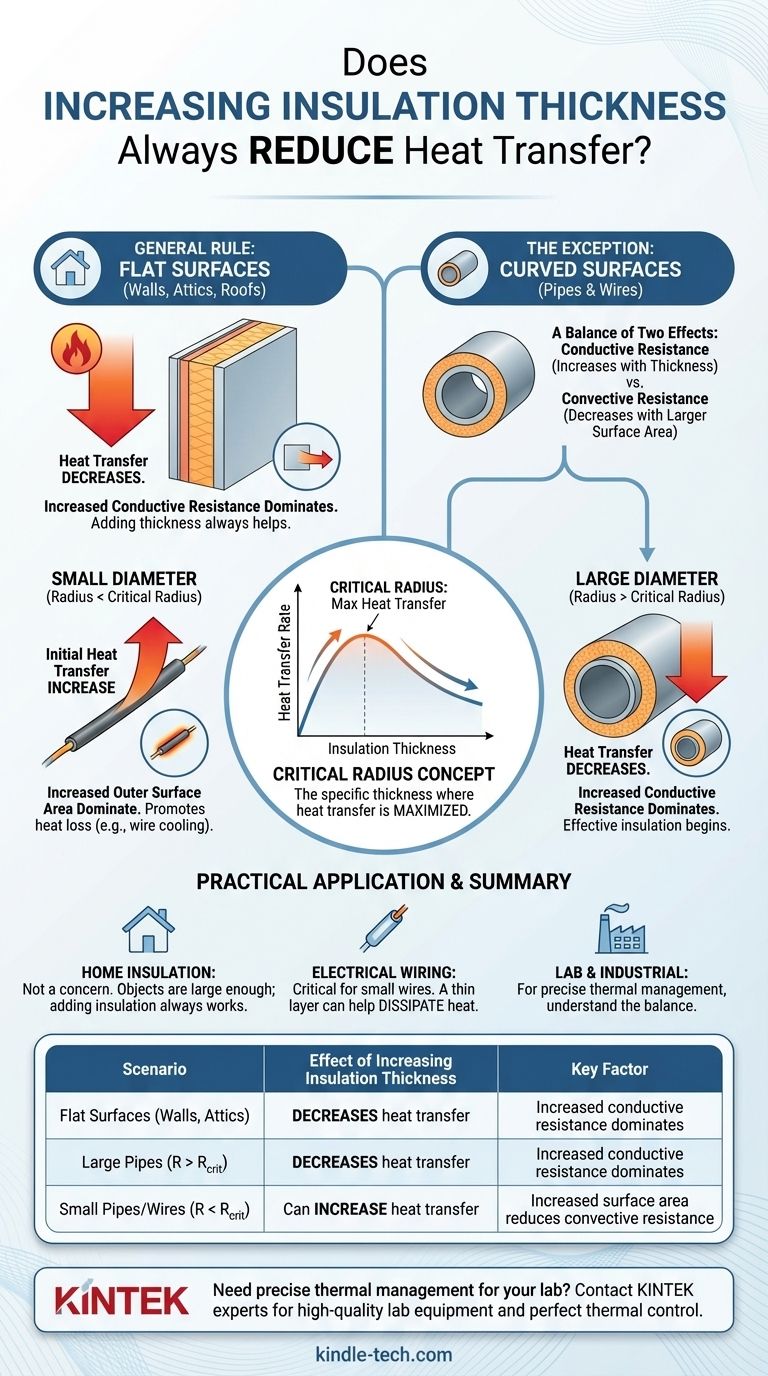
Na quase totalidade das aplicações comuns, aumentar a espessura do seu isolamento diminuirá a taxa de transferência de calor. Este é o propósito fundamental do isolamento. No entanto, para superfícies curvas com um diâmetro muito pequeno, como fios elétricos ou tubulações pequenas, existe um cenário contraintuitivo em que adicionar uma fina camada de isolamento pode, na verdade, aumentar a taxa de transferência de calor devido a um princípio conhecido como raio crítico de isolamento.

A eficácia do isolamento depende do equilíbrio entre dois efeitos concorrentes: a resistência do calor que flui através do material (condução) e a facilidade com que o calor escapa da sua superfície externa (convecção). Para a maioria dos fins práticos, como isolar uma casa, adicionar espessura é sempre útil.

O Objetivo Fundamental do Isolamento: Adicionar Resistência

Para entender como o isolamento funciona, é útil pensar no fluxo de calor como a eletricidade. O calor, como a corrente, sempre seguirá o caminho de menor resistência. A função do isolamento é adicionar resistência térmica a esse caminho.

Compreendendo a Resistência Térmica

A transferência de calor é retardada pela resistência térmica. Quanto maior a resistência total, menor a taxa de transferência de calor. A eficácia do isolamento é medida pelo seu valor R, que é uma medida direta da sua resistência térmica.

Os Dois Tipos de Resistência em Jogo

Quando você isola um objeto, você está manipulando duas formas principais de resistência:

1. Resistência Condutiva: Esta é a resistência ao fluxo de calor através do material isolante sólido. Aumenta diretamente com a espessura. Mais material significa um caminho mais longo para o calor viajar, o que significa maior resistência.
2. Resistência Convectiva: Esta é a resistência à transferência de calor da superfície externa do isolamento para o ar circundante. Essa resistência diminui à medida que a área da superfície aumenta, pois uma superfície maior oferece mais área para o calor escapar.

Por Que a Espessura Importa de Forma Diferente Para Paredes vs. Tubos

A geometria da superfície que você está isolando determina como essas duas resistências interagem. Esta é a chave para entender por que a resposta à pergunta pode ser complexa.

Para Superfícies Planas (Paredes, Sótãos, Telhados)

Quando você adiciona isolamento a uma superfície plana como uma parede, você aumenta significativamente a resistência condutiva.

No entanto, a área da superfície externa permanece praticamente inalterada. Portanto, a resistência convectiva não é afetada. O resultado líquido é simples: a resistência total aumenta e a transferência de calor diminui.

Para Superfícies Curvas (Tubos e Fios)

Ao adicionar isolamento em torno de um tubo ou fio, você está fazendo duas coisas ao mesmo tempo:

1. Você aumenta a resistência condutiva ao adicionar espessura de material (o que reduz a transferência de calor).
2. Você aumenta a área da superfície externa, o que diminui a resistência convectiva (o que promove a transferência de calor).

Esses dois efeitos trabalham um contra o outro. O vencedor desta "queda de cabo de guerra" determina se a taxa líquida de transferência de calor aumenta ou diminui.

O Conceito de Raio Crítico

O raio crítico de isolamento é o raio externo específico no qual a taxa de transferência de calor está no seu máximo absoluto.

• Se o raio original do tubo for menor que o raio crítico: Adicionar isolamento inicialmente aumentará a perda de calor. O efeito negativo da área de superfície crescente (menor resistência convectiva) supera o efeito positivo da espessura adicionada (maior resistência condutiva).
• Se o raio original do tubo for maior que o raio crítico: Adicionar isolamento começará imediatamente a diminuir a perda de calor, como deveria. O benefício da maior resistência condutiva é dominante desde o início.

Compreendendo os Compromissos: Raio Crítico na Prática

Embora este fenômeno seja um conceito importante na física da transferência de calor, sua aplicação prática é limitada a cenários específicos.

Quando o Raio Crítico é uma Preocupação Real?

O efeito do raio crítico é relevante principalmente para objetos com diâmetro muito pequeno. Para materiais isolantes típicos, o raio crítico é frequentemente de apenas alguns milímetros.

Isso o torna um fator no projeto de fiação elétrica, onde o objetivo é frequentemente dissipar o calor para evitar o superaquecimento. Um revestimento fino de isolamento pode, na verdade, ajudar a resfriar o fio de forma mais eficaz do que se estivesse nu. É também uma consideração para tubulações de processo de diâmetro muito pequeno, como linhas de traçador de vapor.

Por Que Raramente é um Problema para o Isolamento Doméstico

Para quase todas as aplicações domésticas e comerciais, os objetos que estão sendo isolados já são muito maiores do que o raio crítico.

Um tubo de encanamento padrão, um duto de HVAC ou um aquecedor de água é grande demais para que esse efeito seja uma preocupação. Para esses itens, você já está "além do pico", e adicionar qualquer quantidade de isolamento diminuirá de forma confiável a transferência de calor e economizará energia.

Fazendo a Escolha Certa para o Seu Objetivo

Sua abordagem ao isolamento deve ser guiada pela sua aplicação específica e resultado desejado.

• Se o seu foco principal for isolar sua casa (paredes, sótão, tubos grandes): Adicionar mais isolamento diminuirá de forma confiável a transferência de calor e reduzirá as contas de energia. O raio crítico não é uma preocupação prática.
• Se o seu foco principal for o projeto para tubos de pequeno diâmetro ou fios elétricos: Você deve calcular o raio crítico para garantir que seu isolamento esteja alcançando o efeito desejado, seja ele reter ou dissipar calor.
• Se o seu foco principal for simplesmente entender a física: Lembre-se de que a transferência total de calor é determinada pelo equilíbrio entre condução (resistida pela espessura) e convecção (auxiliada pela área da superfície).

Compreender esse equilíbrio entre a resistência do material e a área da superfície permite que você use o isolamento de forma eficaz em qualquer cenário.

Tabela de Resumo:

Cenário	Efeito do Aumento da Espessura do Isolamento	Fator Chave
Superfícies Planas (Paredes, Sótãos)	Diminui a transferência de calor	A resistência condutiva aumentada domina
Tubos Grandes (Raio > Raio Crítico)	Diminui a transferência de calor	A resistência condutiva aumentada domina
Tubos Pequenos/Fios (Raio < Raio Crítico)	Pode aumentar a transferência de calor	O aumento da área de superfície reduz a resistência convectiva

Precisa de gerenciamento térmico preciso para seu equipamento de laboratório? Compreender os princípios de transferência de calor é crucial para manter condições ideais para instrumentos e experimentos sensíveis. A KINTEK é especializada em fornecer equipamentos e consumíveis de laboratório de alta qualidade projetados para eficiência e confiabilidade. Se você está isolando um reator ou selecionando o forno certo, nossa experiência pode ajudá-lo a alcançar o controle térmico perfeito. Entre em contato com nossos especialistas hoje mesmo para discutir suas necessidades específicas de laboratório e aprimorar o desempenho do seu laboratório.