Em resumo, uma área maior diminui a pressão exercida pela mesma força. A relação é inversamente proporcional: à medida que a área sobre a qual uma força constante é aplicada aumenta, a pressão em qualquer ponto dessa superfície diminui. Isso ocorre porque a mesma quantidade de força está sendo distribuída por uma superfície mais ampla.
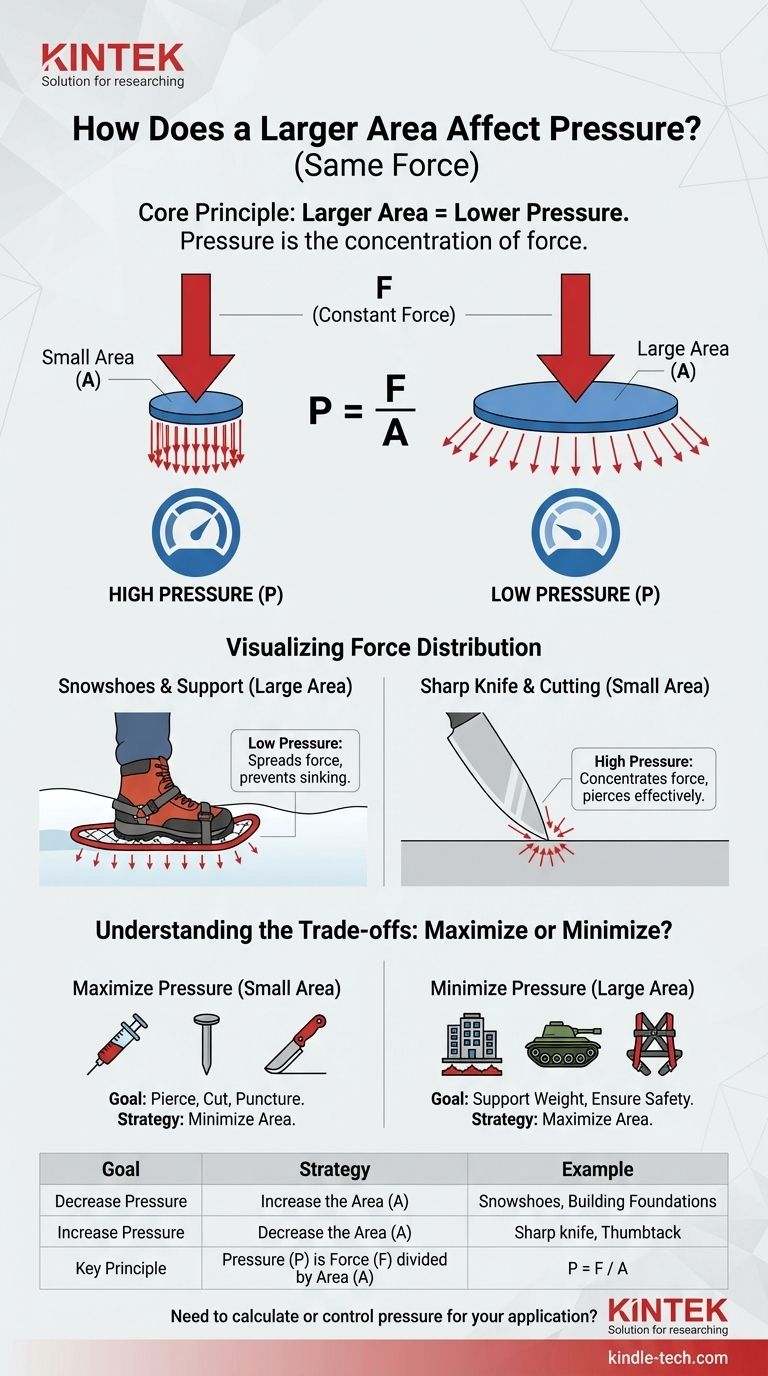
O princípio central a ser compreendido é que pressão não é a força em si, mas a concentração da força. Ao aumentar a área de contato, você está efetivamente diluindo a força, levando a uma redução na pressão.
A Relação Fundamental: Pressão, Força e Área
Para realmente compreender este conceito, devemos observar a física simples, mas poderosa, por trás dele. A interação entre esses três elementos governa tudo, desde como uma faca corta até como um edifício se sustenta.
A Equação Central
A relação é definida pela equação P = F / A.
- P significa Pressão, que é a quantidade de força exercida por unidade de área.
- F significa Força, que é o empurrão ou puxão em um objeto (como o peso).
- A significa Área, que é a superfície sobre a qual a força é distribuída.
Esta fórmula deixa claro que, se a Força (F) permanecer constante, aumentar a Área (A) no denominador inevitavelmente fará com que a Pressão (P) resultante diminua.
Uma Analogia Intuitiva: Cama de Pregos
Imagine tentar ficar em pé sobre um único prego. Todo o peso do seu corpo (a força) seria concentrado no minúsculo ponto daquele prego, criando uma pressão imensa que facilmente perfuraria seu pé.
Agora, imagine uma cama de milhares de pregos. Quando você se deita, o mesmo peso do seu corpo é distribuído uniformemente pelos pontos de todos esses pregos. A área total é enorme, então a pressão de qualquer prego individual é incrivelmente pequena e insuficiente para romper sua pele. A força não mudou, mas a área sim, mudando radicalmente o resultado.
Visualizando a Distribuição de Força
Pense na força como uma quantidade fixa de água e na área como o recipiente onde você a despeja.
Se você despejar a água em um copo alto e fino (uma área pequena), o nível da água será alto (pressão alta). Se você despejar a mesma quantidade de água em uma bandeja larga e rasa (uma área grande), o nível da água será muito baixo (pressão baixa). A quantidade de água nunca mudou, apenas sua concentração.
Exemplos Práticos no Dia a Dia
Este princípio não é apenas teórico; é um aspecto fundamental da engenharia e do design com o qual você interage constantemente.
Por Que as Raquetes de Neve Funcionam
O peso de uma pessoa (força) é constante. Ao usar uma bota normal, essa força é concentrada na pequena área da sola, fazendo com que você afunde na neve. As raquetes de neve aumentam drasticamente a área da superfície, distribuindo seu peso e diminuindo a pressão muito abaixo do que a neve pode suportar.
O Corte de uma Faca
Uma faca afiada tem uma área de superfície extremamente pequena em sua borda de corte. Esse design concentra a força que você aplica, criando uma pressão imensa que pode fatiar materiais facilmente. Uma faca cega tem uma área maior e cega, que espalha a força e exige muito mais esforço para atingir a mesma pressão de corte.
Fundações de Edifícios
Arranha-céus são incrivelmente pesados. Para evitar que afundem no solo, eles são construídos sobre fundações de concreto largas e maciças. Essas fundações espalham o imenso peso (força) do edifício por uma área muito grande, garantindo que a pressão exercida sobre o solo seja baixa o suficiente para ser suportada com segurança.
Alfinetes e Agulhas
Um alfinete de desenho é um exemplo perfeito de manipulação desse princípio. Ele tem uma cabeça grande e plana para o seu polegar (área grande, baixa pressão para conforto) e uma ponta afiada e minúscula para a parede (área pequena, alta pressão para perfuração fácil).
Compreendendo as Compensações
O objetivo nem sempre é diminuir a pressão. O design ideal depende inteiramente da função pretendida, e os engenheiros devem escolher se devem concentrar ou distribuir a força.
Quando a Alta Pressão é o Objetivo
Em muitas aplicações, o objetivo é maximizar a pressão. Isso é alcançado minimizando a área de contato para concentrar a força aplicada.
Exemplos incluem agulhas de injeção, pregos, ferramentas de corte e lâminas de patins de gelo. O propósito de todo o design dessas ferramentas é criar uma pressão alta o suficiente para perfurar uma superfície com força mínima.
Quando a Baixa Pressão é Crítica
Inversamente, minimizar a pressão é frequentemente uma questão de segurança, estabilidade ou preservação. Isso é alcançado maximizando a área de contato.
Exemplos incluem as esteiras largas de um tanque ou trator, as alças largas de uma mochila pesada e os cintos de segurança que distribuem a força de uma queda pelo tronco.
Fazendo a Escolha Certa para o Seu Objetivo
Compreender como manipular a relação entre força, pressão e área é fundamental para resolver inúmeros desafios físicos.
- Se o seu foco principal é perfurar, cortar ou furar: Você deve concentrar sua força tornando a área de contato a menor possível.
- Se o seu foco principal é suportar peso ou evitar afundamento: Você deve distribuir sua força tornando a área de contato a maior possível.
- Se o seu foco principal é garantir a segurança durante um impacto: Você deve dissipar a força pela área mais ampla possível para minimizar a pressão em qualquer ponto único.
Dominar este único princípio permite que você projete e construa ferramentas mais eficazes e estruturas mais seguras.
Tabela de Resumo:
| Objetivo | Estratégia | Exemplo |
|---|---|---|
| Diminuir a Pressão | Aumentar a Área (A) | Raquetes de neve, fundações de edifícios |
| Aumentar a Pressão | Diminuir a Área (A) | Faca afiada, alfinete de desenho, lâmina de patins de gelo |
| Princípio Chave | Pressão (P) é Força (F) dividida pela Área (A) | P = F / A |
Precisa calcular ou controlar a pressão para sua aplicação? A KINTEK é especializada em equipamentos de laboratório e consumíveis, fornecendo as ferramentas e a experiência para ajudá-lo a aplicar esses princípios fundamentais em sua pesquisa ou processos de controle de qualidade. Quer você esteja projetando um novo produto ou otimizando um procedimento, nossa equipe pode ajudá-lo a selecionar o equipamento certo para medir e gerenciar força e pressão com precisão.
Entre em contato com nossos especialistas hoje mesmo para discutir suas necessidades específicas!
Guia Visual
