Qual é a relação entre as forças em um sistema hidráulico? Desvende o Poder da Multiplicação de Força

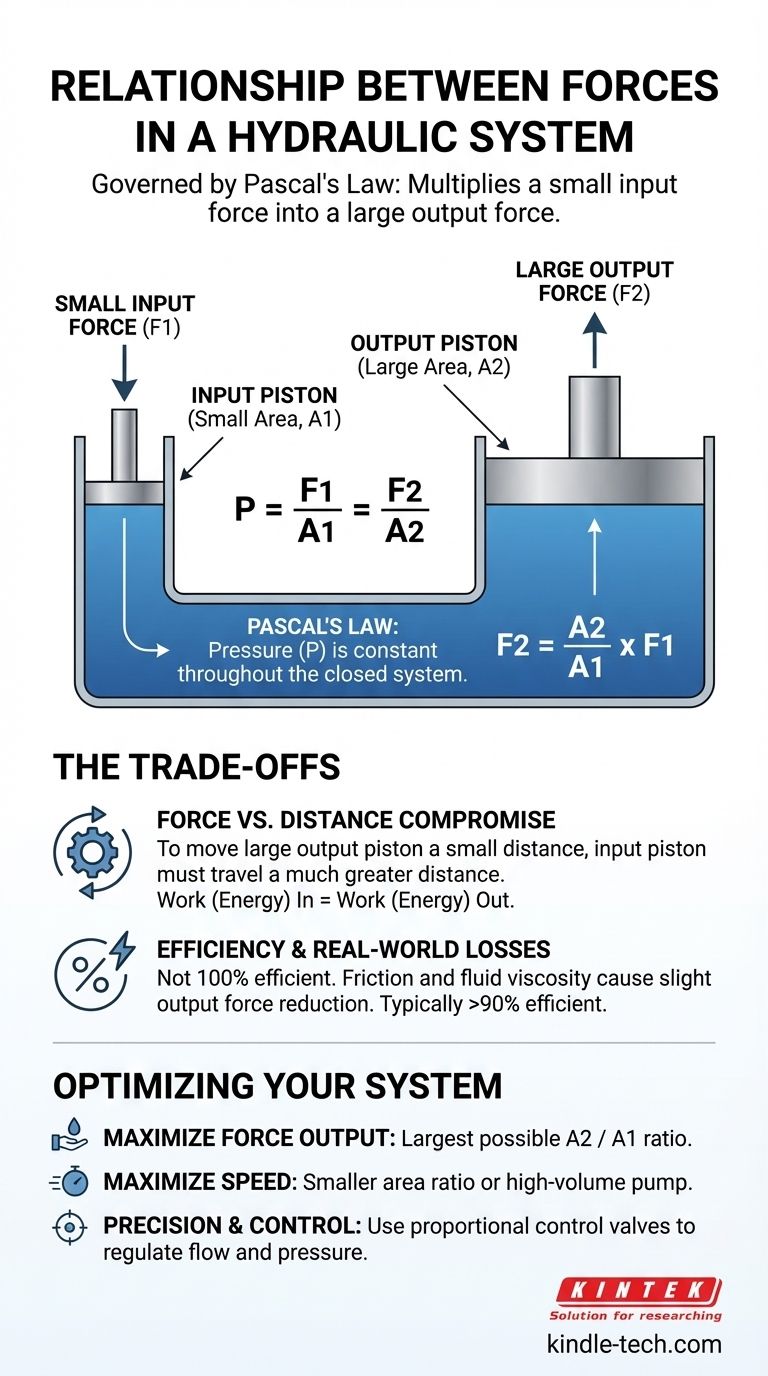
Em sua essência, a relação entre as forças em um sistema hidráulico é governada pela Lei de Pascal, que permite que uma pequena força de entrada seja multiplicada em uma força de saída significativamente maior. Este princípio de multiplicação de força é alcançado aplicando pressão a um fluido confinado e incompressível, como óleo.

A relação fundamental é que a pressão permanece constante em todo um sistema hidráulico fechado. Ao manipular a área de superfície sobre a qual essa pressão atua, você pode trocar diretamente uma pequena força aplicada sobre uma pequena área por uma grande força gerada sobre uma grande área.

O Princípio Central: Lei de Pascal

Toda a base da energia hidráulica repousa sobre um princípio simples descoberto no século XVII. Compreender isso é fundamental para entender como todas as máquinas hidráulicas, desde os freios de um carro até uma prensa de 300 toneladas, operam.

O que é a Lei de Pascal?

A Lei de Pascal afirma que uma mudança de pressão em qualquer ponto de um fluido confinado e incompressível é transmitida igualmente por todo o fluido. Em termos mais simples, se você empurrar o fluido em um ponto, a pressão em todos os lugares dentro do recipiente aumenta na mesma quantidade.

O Papel da Pressão

A pressão é definida como Força dividida pela Área (P = F/A). Esta fórmula simples é a chave para desbloquear a multiplicação de força. Ao controlar a área, você pode influenciar diretamente a força.

Como a Força é Multiplicada

Imagine um recipiente selado com dois pistões de tamanhos diferentes: um pequeno pistão de entrada (Área 1) e um grande pistão de saída (Área 2).

Quando você aplica uma pequena força (Força 1) ao pequeno pistão, você gera pressão (Pressão = Força 1 / Área 1).

Como essa pressão é transmitida igualmente por todo o fluido, a mesma pressão empurra o grande pistão de saída. Isso cria uma força de saída muito maior (Força 2 = Pressão x Área 2).

Como a pressão é a mesma, podemos dizer F1/A1 = F2/A2. Esta equação mostra que a força de saída (F2) é diretamente proporcional à razão das áreas. Se o pistão de saída tiver 10 vezes a área do pistão de entrada, você obtém 10 vezes a força.

Compreendendo as Compensações

A multiplicação de força não cria energia do nada. Essa poderosa vantagem vem com compromissos inerentes que são críticos para entender em qualquer aplicação prática.

A Compensação entre Força e Distância

A compensação mais significativa é entre a força e a distância que o pistão deve percorrer. Para mover o grande pistão de saída uma pequena distância, o pequeno pistão de entrada deve ser empurrado uma distância muito maior.

O trabalho (Energia) é calculado como Força vezes Distância. O trabalho realizado no lado da entrada deve ser igual ao trabalho realizado no lado da saída (ignorando o atrito). Se você multiplicar a força por 10, você também deve multiplicar a distância de curso do pistão de entrada por 10 para alcançar o mesmo curso de saída.

Eficiência e Perdas no Mundo Real

A fórmula F1/A1 = F2/A2 descreve um sistema perfeito e sem atrito. Na realidade, você sempre terá perdas de eficiência.

O atrito entre as vedações e as paredes do cilindro, bem como o atrito interno (viscosidade) do fluido hidráulico, reduzirão ligeiramente a força de saída real. Um sistema bem projetado é tipicamente mais de 90% eficiente, mas nunca é 100% perfeito.

O Elemento de Controle

Poder bruto é inútil sem a capacidade de gerenciá-lo. Simplesmente aplicar força a um pistão não oferece precisão sobre a velocidade ou magnitude dessa força.

É aqui que componentes como válvulas de controle proporcional e controles de bomba proporcional se tornam essenciais. Eles não geram a força, mas regulam precisamente a taxa de fluxo e a pressão do fluido, permitindo que um operador controle finamente a velocidade e a força do atuador hidráulico para tarefas complexas.

Fazendo a Escolha Certa para o Seu Objetivo

Compreender essa relação de força permite avaliar o projeto do sistema com base em seu objetivo principal.

• Se o seu foco principal é maximizar a saída de força: O objetivo é projetar um sistema com a maior razão possível entre a área de saída e a área de entrada.
• Se o seu foco principal é a velocidade: Pode ser necessário aceitar um fator de multiplicação de força menor (uma razão de área menor) ou utilizar uma bomba de alto volume para mover a quantidade necessária de fluido mais rapidamente.
• Se o seu foco principal é precisão e controle: A vantagem mecânica é apenas metade da equação; a eficácia do seu sistema dependerá de válvulas e controles de alta qualidade para modular com precisão a pressão e o fluxo hidráulico.

Compreender esse equilíbrio entre pressão, área e deslocamento é o primeiro passo para dominar a aplicação da energia hidráulica.

Tabela Resumo:

Conceito	Fórmula Chave	Implicação Prática
Lei de Pascal	A pressão é transmitida igualmente	Pequena força de entrada cria grande força de saída
Multiplicação de Força	F1/A1 = F2/A2	A força de saída escala com a razão da área
Compensação	Trabalho de Entrada = Trabalho de Saída	Aumento da força requer aumento da distância de entrada
Eficiência	Tipicamente >90%	Sistemas reais consideram perdas por atrito

Pronto para aproveitar a energia hidráulica precisa para o seu laboratório? Na KINTEK, somos especializados em equipamentos e consumíveis de laboratório de alto desempenho, garantindo que seus sistemas hidráulicos operem com máxima eficiência e controle. Se você precisa de componentes confiáveis ou de aconselhamento especializado sobre multiplicação de força para suas aplicações, nossa equipe está aqui para ajudar. Entre em contato conosco hoje para otimizar suas soluções hidráulicas!

Guia Visual