Cálculo teórico da pressão negativa
Formulação e variáveis
O cálculo teórico da pressão negativa para ventosas é regido pela fórmula:
[ P_{\text{max}} = \frac{10F}{S} ]
onde:
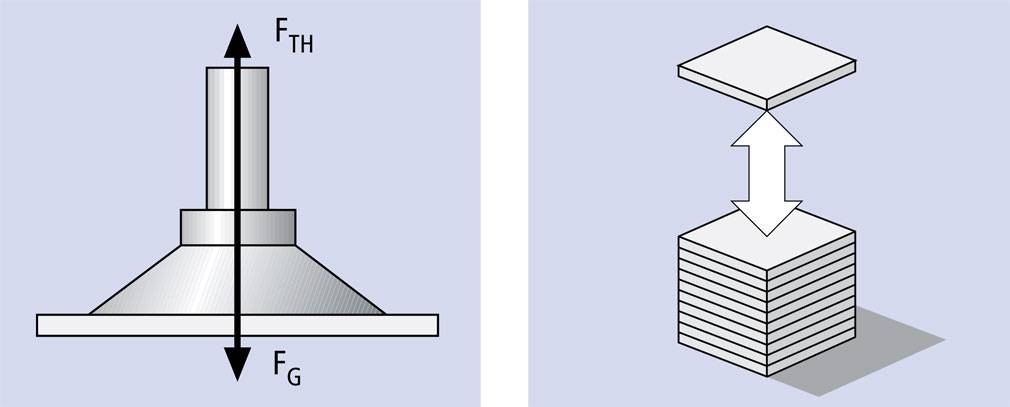
- ( F ) representa a força de adsorção teórica, medida em Newtons (N).
- ( P_{\text{max}} ) representa a pressão negativa máxima que pode ser atingida, expressa em quilopascal (kPa).
- ( S ) é a área de contacto entre a ventosa e o objeto, quantificada em centímetros quadrados (cm²).
Esta fórmula fornece uma compreensão fundamental da forma como a pressão negativa máxima teórica é derivada, o que é essencial para selecionar bombas de vácuo adequadas e garantir uma adsorção eficaz do objeto.
Limitações em aplicações práticas
Em aplicações práticas, os cálculos teóricos da pressão negativa nem sempre se traduzem diretamente em desempenho no mundo real. Devem ser tidos em conta vários factores críticos para garantir o funcionamento eficaz das bombas de vácuo, particularmente em cenários que envolvem a adsorção de objectos.
Em primeiro lugar, vedação do sistema desempenha um papel fundamental. Mesmo pequenas fugas no sistema podem reduzir significativamente a força de sucção real. Isto deve-se ao facto de qualquer falha na vedação permitir a infiltração de ar no sistema, contrariando a pressão negativa gerada pela bomba de vácuo. Consequentemente, a eficácia das ventosas pode ser comprometida, levando a potenciais falhas na manutenção da adsorção de objectos.
Em segundo lugar, adesão à superfície é outra consideração crucial. A capacidade da ventosa para aderir à superfície do objeto não depende apenas da pressão negativa, mas também das caraterísticas da superfície. As superfícies lisas e não porosas proporcionam geralmente uma melhor aderência, enquanto as superfícies rugosas ou porosas podem reduzir a área de contacto, diminuindo assim a força de sucção. Esta variabilidade na aderência da superfície requer uma abordagem mais diferenciada na seleção da bomba de vácuo.
Por fim, margens de segurança são essenciais para ter em conta as incertezas e variações nas condições do mundo real. Os cálculos teóricos assumem frequentemente condições ideais, o que pode não ser verdade em aplicações práticas. Por conseguinte, a incorporação de margens de segurança assegura que a bomba de vácuo pode lidar com flutuações inesperadas na pressão, no caudal e nas condições da superfície. Esta medida de precaução é particularmente importante em aplicações críticas em que uma falha pode ter consequências significativas.
Em resumo, embora os cálculos teóricos forneçam uma compreensão fundamental da pressão negativa, as aplicações práticas requerem uma consideração abrangente da vedação do sistema, da adesão da superfície e das margens de segurança para garantir uma força de sucção fiável e eficaz.
Considerações práticas na seleção da bomba de vácuo
Importância do caudal
O caudal real da bomba de vácuo é um parâmetro crítico que influencia diretamente a eficiência e a fiabilidade do processo de adsorção de objectos. Esta métrica torna-se especialmente significativa quando se aborda a questão da fuga de ar entre a ventosa e a superfície do objeto. As fugas de ar podem comprometer a pressão de vácuo, reduzindo assim a eficácia da força de sucção e conduzindo potencialmente a falhas na manutenção da aderência.
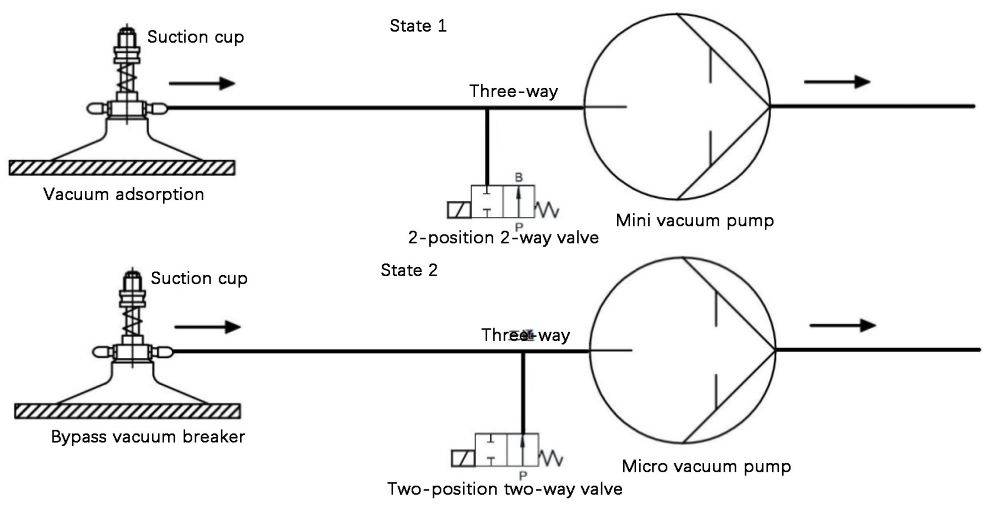
Para compreender melhor o impacto do caudal, é essencial considerar os seguintes pontos-chave:
-
Gestão de fugas de ar: Os caudais elevados ajudam a compensar rapidamente qualquer entrada de ar, mantendo o nível de vácuo necessário. Isto é particularmente importante em aplicações em que a superfície do objeto não é perfeitamente lisa ou quando existem pequenas deformações que podem levar à infiltração de ar.
-
Desempenho dinâmico: Em ambientes dinâmicos onde os objectos estão a ser movidos ou rodados, um caudal mais elevado assegura que a pressão de vácuo é mantida de forma consistente. Esta estabilidade dinâmica é crucial para tarefas que requerem um manuseamento de precisão, tais como linhas de montagem automatizadas ou braços robóticos.
-
Eficiência do sistema: Uma bomba de vácuo com um caudal ideal não só melhora o desempenho do sistema, como também contribui para a eficiência energética. Ao manter um nível de vácuo estável com um consumo mínimo de energia, os custos operacionais globais podem ser significativamente reduzidos.
Em resumo, a seleção de uma bomba de vácuo com o caudal adequado não se trata apenas de cumprir normas teóricas, mas também de garantir robustez e fiabilidade práticas em aplicações do mundo real. Esta consideração é vital para as indústrias que dependem do manuseamento preciso e consistente de objectos, onde mesmo pequenas discrepâncias na pressão de vácuo podem levar a desafios operacionais significativos.
Segurança e margens de erro
Para garantir que a bomba de vácuo cumpre as rigorosas exigências da sua aplicação, é imperativo selecionar modelos com caudais reais generosos e pressões negativas elevadas. Esta abordagem proactiva tem em conta os potenciais desvios e flutuações que podem surgir durante o funcionamento.
| Considerações | Impacto nas margens de segurança |
|---|---|
| Caudal | Assegura uma sucção adequada mesmo com pequenas fugas de ar. |
| Pressão negativa | Fornece um amortecedor contra variações na adesão da superfície e na vedação do sistema. |
Ao optar por bombas com capacidades melhoradas, os utilizadores podem lidar com as incertezas de forma mais eficaz, salvaguardando assim a integridade e a fiabilidade do sistema de vácuo.
Produtos relacionados
- Bomba de Vácuo Rotativa de Palhetas de Laboratório para Uso em Laboratório
- Bomba de Vácuo Vertical de Circulação de Água para Laboratório
- Bomba de Vácuo de Circulação de Água de Bancada para Uso em Laboratório
- Fole de Vácuo para Conexão Eficiente e Vácuo Estável em Sistemas de Alto Desempenho
- Refrigerador de Armadilha Fria a Vácuo Armadilha Fria Indireta
Artigos relacionados
- Como escolher o melhor evaporador rotativo (Rotavapor) para o seu orçamento
- Erros comuns a evitar quando se utiliza um evaporador de vácuo rotativo
- Instalação do Tê de encaixe do forno tubular
- Compreender os princípios básicos de um evaporador rotativo
- Escolher o evaporador de vácuo rotativo certo para o seu laboratório
