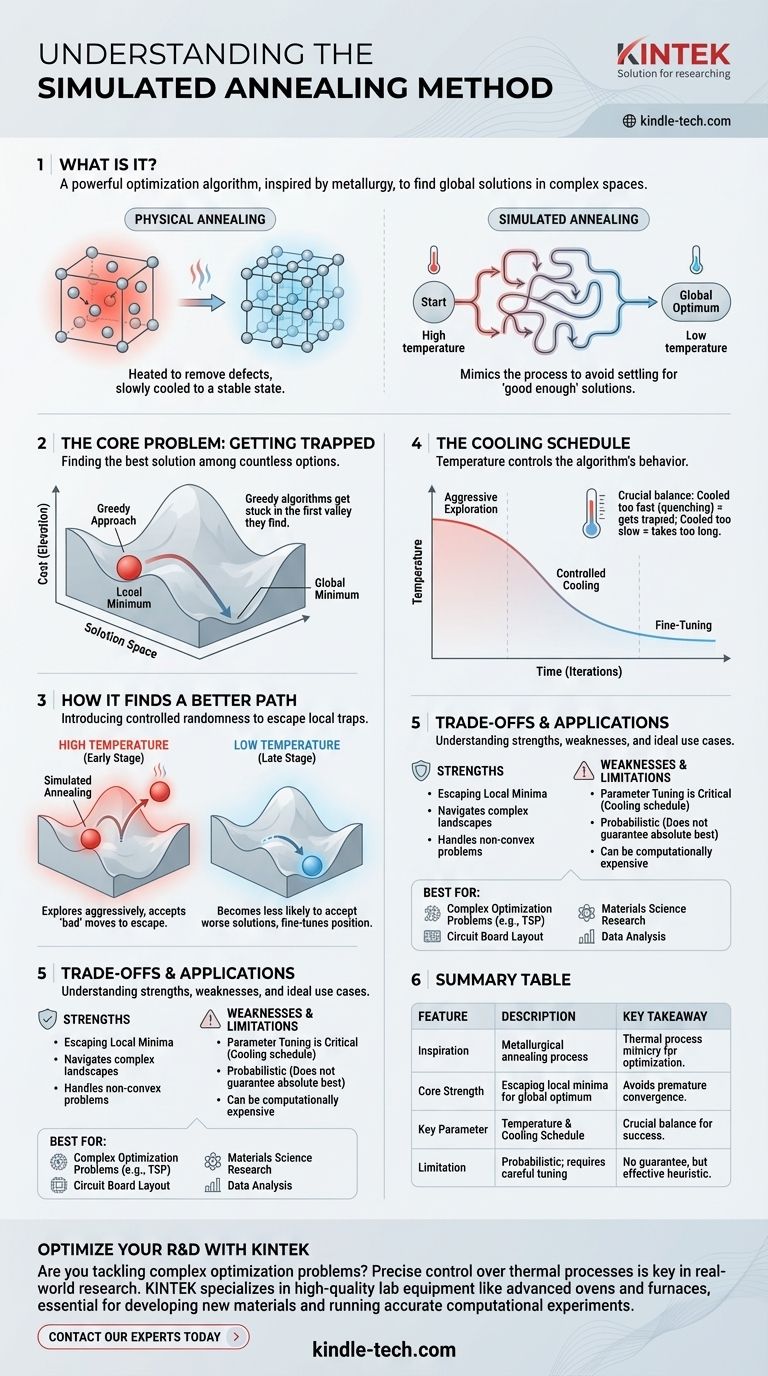
Em resumo, o recozimento simulado é um poderoso algoritmo de otimização usado para encontrar uma boa (e frequentemente global) solução em um espaço de busca vasto e complexo. É diretamente inspirado no processo metalúrgico de recozimento, onde um material é aquecido e depois resfriado lentamente para remover defeitos e atingir um estado cristalino estável de baixa energia. O algoritmo imita este processo físico para resolver problemas computacionais abstratos.
Em sua essência, o recozimento simulado evita a armadilha comum de se contentar com uma solução "boa o suficiente", imitando o processo físico de recozimento de metais. Ele começa explorando uma ampla gama de possibilidades (alta temperatura) e gradualmente restringe seu foco a uma solução estável e de alta qualidade (baixa temperatura).
O Problema Central: Ficar Preso
Para entender o recozimento simulado, você deve primeiro entender o problema que ele resolve: encontrar a melhor solução possível entre inúmeras opções, uma tarefa conhecida como otimização.
A Paisagem das Soluções
Imagine que cada solução possível para o seu problema é um ponto em uma vasta paisagem montanhosa. A elevação de cada ponto representa seu "custo" — quanto menor a elevação, melhor a solução. Seu objetivo é encontrar o ponto mais baixo em todo o mapa, o mínimo global.
A Abordagem "Gananciosa" e Sua Falha
Um algoritmo simples, frequentemente chamado de escalada de colina (hill-climbing), começaria em um ponto aleatório e sempre se moveria para baixo. Esta é uma abordagem "gananciosa" porque aceita apenas movimentos que proporcionam melhoria imediata.
O problema é que este método ficará preso no primeiro vale que encontrar — um mínimo local. Ele não tem como saber se um vale muito mais profundo, o mínimo global, existe logo depois da próxima colina.
Como o Recozimento Simulado Encontra um Caminho Melhor
O recozimento simulado supera essa limitação introduzindo um elemento controlado de aleatoriedade que lhe permite escapar dessas armadilhas locais.
A Inspiração: Recozimento Físico
Na metalurgia, aquecer um metal dá aos seus átomos energia suficiente para se moverem livremente, saindo de estruturas subótimas e defeituosas. À medida que o metal é resfriado lentamente, os átomos têm tempo para se estabelecerem em uma rede cristalina altamente ordenada e forte — um estado de energia mínima.
O Algoritmo: Temperatura como Botão de Controle
O recozimento simulado adota este conceito introduzindo um parâmetro de temperatura. Esta não é uma temperatura física, mas uma variável que controla o comportamento do algoritmo.
O algoritmo começa com uma alta temperatura. Neste estado, ele explora a paisagem de soluções agressivamente, muito parecido com os átomos energéticos em metal quente. Ele tem uma alta probabilidade de aceitar movimentos que são piores do que sua posição atual. Esta é a chave: fazer um movimento "ruim" é o que lhe permite sair de um mínimo local.
O Cronograma de Resfriamento
À medida que o algoritmo é executado, a temperatura é gradualmente diminuída de acordo com um cronograma de resfriamento. À medida que a temperatura diminui, o algoritmo se torna cada vez menos propenso a aceitar uma solução pior.
No final, a uma temperatura muito baixa, o algoritmo se comporta como o método simples de escalada de colina, aceitando apenas melhorias e ajustando sua posição no que é, esperançosamente, o mínimo global.
Compreendendo as Trocas
Como qualquer ferramenta poderosa, o recozimento simulado não é uma solução universal. Compreender suas limitações é fundamental para usá-lo de forma eficaz.
Força: Escapar de Mínimos Locais
Sua principal vantagem é a capacidade de navegar por paisagens complexas e não convexas com muitos mínimos locais. Para problemas onde algoritmos gananciosos falham consistentemente, o recozimento simulado é uma excelente escolha.
Fraqueza: A Sintonização de Parâmetros é Crítica
O desempenho do algoritmo é altamente sensível ao cronograma de resfriamento. Se resfriado muito rapidamente, ele pode ficar preso em um mínimo local de qualquer maneira ("têmpera"). Se resfriado muito lentamente, pode levar uma quantidade impraticável de tempo para encontrar uma solução. Encontrar o cronograma certo geralmente requer experimentação.
Limitação: É um Método Probabilístico
O recozimento simulado não garante que encontrará a melhor solução absoluta (o mínimo global). É uma heurística, o que significa que é projetado para encontrar uma solução muito boa em um tempo razoável. Há sempre uma chance estatística de que ele se estabeleça em um estado subótimo.
Fazendo a Escolha Certa para o Seu Problema
Use esta orientação para decidir se o recozimento simulado é a abordagem correta para sua tarefa de otimização.
- Se seu foco principal é resolver um problema complexo com muitas armadilhas (mínimos locais): O recozimento simulado é uma das melhores ferramentas para o trabalho, especialmente para problemas clássicos como o Problema do Caixeiro Viajante ou o layout de placas de circuito.
- Se seu foco principal é encontrar uma solução comprovadamente ótima com velocidade máxima: Você deve primeiro verificar se seu problema é simples o suficiente (por exemplo, convexo) para ser resolvido por um algoritmo mais rápido e determinístico, como programação linear ou uma abordagem gananciosa padrão.
Em última análise, o recozimento simulado oferece uma estrutura robusta para navegar em espaços de busca vastos e difíceis para encontrar soluções de alta qualidade onde métodos mais simples falham.
Tabela Resumo:
| Característica | Descrição |
|---|---|
| Inspiração | Processo de recozimento metalúrgico (aquecimento e resfriamento lento) |
| Força Principal | Escapar de mínimos locais para encontrar um ótimo global |
| Parâmetro Chave | Temperatura e Cronograma de Resfriamento |
| Melhor Para | Problemas complexos de otimização com muitas armadilhas locais |
| Limitação | Probabilístico; requer ajuste cuidadoso de parâmetros |
Otimize Sua Pesquisa e Desenvolvimento com a KINTEK
Você está enfrentando problemas complexos de otimização em ciência dos materiais, engenharia química ou análise de dados? Os princípios do recozimento simulado são inspirados em processos térmicos do mundo real, e ter controle preciso sobre esses processos em seu laboratório é crucial.
A KINTEK é especializada em equipamentos de laboratório de alta qualidade, incluindo fornos e estufas avançados que fornecem o aquecimento uniforme e o resfriamento controlado essenciais para pesquisa e desenvolvimento. Seja você desenvolvendo novos materiais ou executando experimentos computacionais, equipamentos confiáveis são a base para resultados precisos.
Entre em contato com nossos especialistas hoje para encontrar a solução de laboratório perfeita para aprimorar seus fluxos de trabalho de otimização e alcançar resultados inovadores.
Guia Visual
Produtos relacionados
As pessoas também perguntam
- O que é um misturador de laboratório? Um Guia para Alcançar a Homogeneidade Perfeita da Amostra
- Como você faz a manutenção de uma batedeira planetária? Um guia proativo para estender a vida útil do equipamento
- Qual é a frequência de um agitador de peneiras? A Chave para uma Análise Precisa do Tamanho das Partículas
- O que é um agitador de peneiras vibratórias? Obtenha uma análise de tamanho de partícula precisa e repetível
- Qual a diferença entre um agitador e um vórtex? Escolha o Misturador Certo para o Fluxo de Trabalho do Seu Laboratório
